Research Areas
Applications in Real-World Networks
Big data and complex networks proliferate, and interest in graph theory is heightening. Problems are diverse and solutions are not obvious. With our results on industry projects involving city planning, smart cars, social networks and computer science, we're building a reputation as leaders in applied graph theory.
Research in Pure Mathematics
We also attack problems of a purely abstract nature, with no express or immediate application. By exploring challenging, theoretical problems, our students refine their analytical rigour, abstract thinking and creativity, while advancing mathematics on a fundamental level.
Every year, we have openings in discrete mathematics research. If you're a student or postdoctoral fellow, contact the supervising professor.

Businesses are continually seeking to optimize their operations. To this end, we build sophisticated mathematical models to help our industrial partners achieve greater organizational efficiencies. In recent years, the demand for solutions has greatly outstripped the supply of tools. Fields-CQAM Lab on Computational Methods in Industrial Mathematics, led by Dr. Pawel Pralat, is working concertedly to close this gap, and our work has been applied in leading companies such as Microsoft, Google and the Government of Canada.
Our mathematical models need to be robust enough to handle real-world scenarios of high combinatorial complexity. We leverage big data, analytics tools such as machine learning, and advance simulation techniques. We build models capable of reflecting all harvested data, imposed business constraints and uncertainty in the given business environment. We also develop new theorems, algorithms, and implementations for non-standard solutions to industrial problems involving systems with hundreds of thousands of computational units.
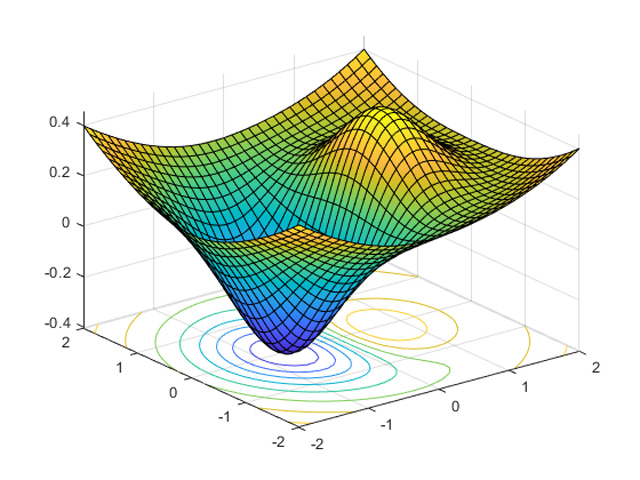
In this area of research, we work on a fundamental subject in theoretical computer science: optimizing a function with limited computational resources. Constraining resources may include, for example, computational power (time), computational space (memory) and centrality of computation (where multiple computing entities exist). As lack of resources may be an overwhelming obstacle, our work investigates the outermost boundaries of computation in a given environment. We quantify the effectiveness of proposed solutions and determine the most favourable.
Within the broad area of Algorithm Design, we also seek to deepen understanding of algorithmic methods, provide new algorithmic techniques, and identify their boundaries in various computation models. Our work also combines elements of and/or finds applications in Combinatorial Optimization, Mathematical Programming, Mobile Agent Computing, Operations Research and Game Theory.
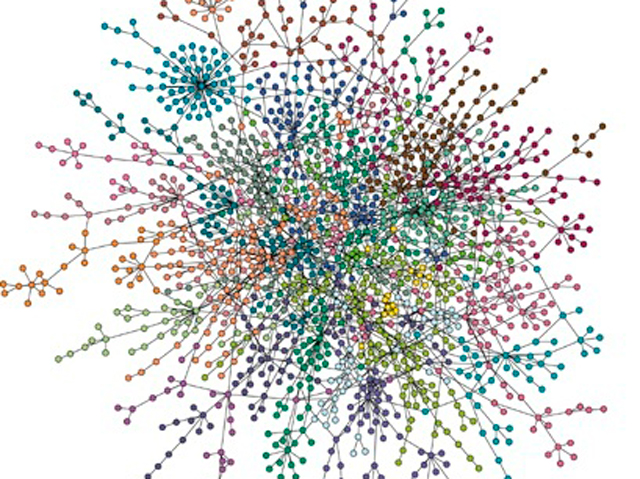
In graph searching, we consider simplified, combinatorial models for detecting and neutralizing an adversary’s activity on a network. The most studied such game is Cops and Robbers, where the cops and robber can only move to vertices with which they share an edge. Cops and Robbers and its variants form an emerging topic in graph theory, with new results rapidly appearing in the literature.
Complex networks pose big data challenges to researchers. For example, Google indexes trillions of pages on the web, and Facebook consists of over one billion user accounts. Mathematical models are powerful tools for simulating properties of complex networks, and analyzing these models also presents fascinating mathematical challenges.

In this area of research, we study graphs generated not by deterministic rules, but by some random process. Although some random networks do not neatly reflect real-world networks – which are typically constructed by sophisticated rules and subject to constraints – they can nonetheless be used to increase understanding of their properties. Random graphs were first modeled by Erdős and Rényi in the 1950s, and their results created strong connections between graph theory and probability theory. Although simple, this classic model has been thoroughly studied, but does not sufficiently address all characteristics of modern, complex networks.
In our research, we have developed new models, such as the Spatial Preferential Attachment Model, that reflect finer, more nuanced details within existing random graph models. With the availability of big data, interest in random graphs has heightened, and numerous applications are now being found, such as modelling the spread of viral diseases, neuronal activity in neural networks and forwarding information packets in computer networks, to name only a few.

In seeking results for deterministic graphs, our research often involves applying probabilistic methods to combinatorial problems. This method often turns out to be very powerful when constructive arguments cannot be applied. Through this nonconstructive proof technique, we are able to demonstrate with certainty that a combinatorial object exists – without having to actually locate the object.
This involves generating a random sample and then proving that the desired property holds with a probability greater than zero. We thus produce an outcome that is equivalent to finding the true answer by exhaustively working through all possibilities instead. Many applications of the probabilistic methods can be found in computer science, particularly in randomized algorithms.
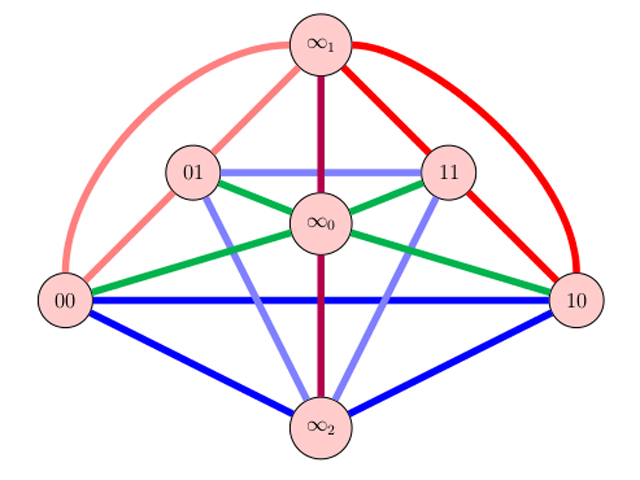
Within the area of design theory, we focus on graph decompositions and covering arrays. We further our understanding of graphs by investigating their substructure and by decomposing the edges of graphs into further structures, or subgraphs. This area of mathematics has classically found applications in statistics and the design of scientific experiments, hence the name.
Our research also considers combinatorial coverings and packings. These structures are used in software testing and to find error correcting/detecting codes. Covering arrays can be used as a template in a testing environment to provide a test suite where all pairs (or t-tuples) are tested in a coherent manner. Packings are useful in the context of codes. Our work has applications in coding theory, discrete scheduling problems, analysis of algorithms, and software and network testing.

In this research areas, we provide a framework for studying fundamental properties of structures found in other areas of mathematics. The field intersects logic, algebra and discrete mathematics. While many applications exist in group theory, ring theory, graph theory and computational complexity, we are currently searching for applications in theoretical computer science. Specifically, we research descriptive complexity of algorithmic problems on finite relational structures, and algorithms capable of solving decision problems on omega-categorical structures.
We are also exploring Gurevich’s Conjecture, one of the most important open questions in descriptive complexity. We are searching for a “universal programming language” capable of handling all decision problems solvable in polynomial time. The current candidates for such languages are based on the principles of dynamic programming, and our work is generating further evidence that they are indeed good candidates capable of solving wide classes of tractable decision problems.